Содержание [Основная идея] Часть I: Теория [Глава 1: Как движутся ИСЗ?] [Глава 2: Какие орбиты и ИСЗ бывают?] Часть II: Практика [Глава 3: Подготовка к наблюдениям] [Глава 4: О времени] [Глава 5: Что и как наблюдать?] §1. Оптические наблюдения Определение орбит ИСЗ Визуальные наблюдения ИСЗ Фото/видео съёмка ИСЗ Фотометрия ИСЗ Наблюдение вспышек ИСЗ Визуальные наблюдения вспышек Фотографирование вспышек Фотометрия ИСЗ за пролёт §2. Радионаблюдения ИСЗ Приём телеметрии ИСЗ Получение снимков облачности [Приложения] [Использованные источники] [Полезные ресурсы сети INTERNET]

Глава 5: Что и как наблюдать? §1. Оптические наблюдения Фотометрия ИСЗ Содержание пункта: Некоторые характеристики движения ИСЗ по небу, влияющие на его яркость. Фазовый угол. Изменение блеска ИСЗ в течении пролёта. Приведенная звёздная величина ИСЗ. Тень Земли. Некоторые характеристики движения ИСЗ по небу, влияющие на его яркость. В этом параграфе будут рассмотрены вопросы любительских фотометрических наблюдений ИСЗ, т.е. количественное измерение оптического излучения (в нашем случае -- отражения) света Солнца от ИСЗ [99]. Основные две цели таких наблюдений -- определение конфигурации панелей солнечных батарей спутников и определение периода вращения некоторых ИСЗ. Кроме этого, также будут рассмотрены некоторые более "экзотические" применения фотометрии ИСЗ, доступные любителям. Для предоставления фотометрии в международном стандарте используется формат "PPAS", расшифровка которого дана в Приложениях. 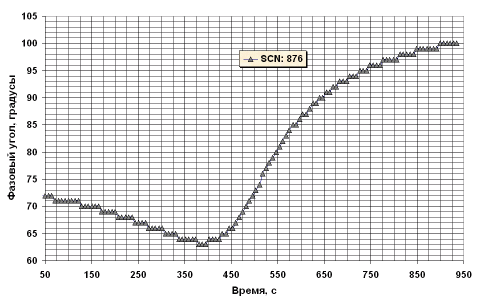Для начала рассмотрим некоторые особенности видимого движения ИСЗ по небу наблюдателя. В качестве примера возьмём первый советский метеорологический спутник, запущенный 28 августа 1964 г. и получивший наименование "Космос-44" (SCN: 876) [94] -- первый метеоспутник из серии "Метеор" [95]. На рис. 1 представлена фотография пятого ИСЗ из серии "Метеор" -- "Космос-122". Рис. 1. ИСЗ "Космос-122" (SCN: 2254) -- пятый метеоспутник серии "Метеор" [95]. Прежде всего посмотрим, как изменяется элевация (угловая высота над горизонтом) спутника -- на рис. 2 представлен график изменения элевации ИСЗ в течении пролёта по небу наблюдателя, расчитанный в "Heavensat". За первый 100 с с момента восхода спутник подымается примерно на 6°, за вторые 100 с -- ещё на 10°, за третьи 100 с -- на 14°, а за четвёртые 100 с -- он подымется ещё на 28°. Как видно, угловая скорость подъёма спутника происходит неравномерно -- сначала медленно, а потом всё быстрее, достигая максимума вблизи точки максимального подъёма (она же будет точкой максимального сближения ИСЗ с наблюдателем). Из этого графика следует, что длина трека ИСЗ на фотографиях (а, значит, и временнОе разрешение) будет разной в разных участках траектории. Рис. 2. Расчитанное в "Heavensat" изменение элевации ИСЗ "Cosmos-44" (SCN: 876) от времени. Время отсчитывается в секундах с момента восхода. [Вверх] Расстояние от ИСЗ до наблюдателя меняется более ожидаемо (см. рис. 3) -- практически линейно, за исключением области наибольшего сближения с наблюдателем. Рис. 3. Расчитанное в "Heavensat" изменение расстояния "Наблюдатель - ИСЗ" от времени для спутника "Cosmos-44" (SCN: 876). Время отсчитывается в секундах с момента восхода. Из графиков выше видно, что чем ближе ИСЗ, тем быстрее он набирает высоту -- факт ожидаемый, т.к. всем знакомо явление перспективы, искажающее реальную скорость перемещение объектов в пространстве. [Вверх] Фазовый угол. 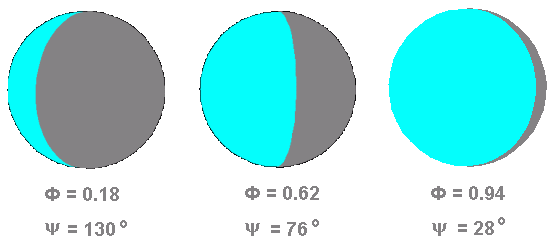Для дальнейшего рассмотрения вопроса об изменении блеска ИСЗ в течении пролёта нужно ознакомиться с понятием фазового угла [96]. Явление фаз луны известно всем -- новолуние, 1-я четверть, полнолуние и 3-я четверть. Однако, для описания видимой освещённой части светила этих четырёх понятий мало, и в астрономии вводится понятие фазы как отношение площади видимой освящённой части светила к площади всего диска. Тогда фаза "0" соответствует новолунию, фаза "0,5" -- первой и третьей четвертям, а фаза "1" -- полнолунию. Но при расчёте блеска ИСЗ важное значение имеет фазовый угол -- угол между центром Солнца, спутником и наблюдателем (см. рис. 4). При ψ = 0° спутник расположен на прямой "Солнце - наблюдатель - ИСЗ", позади наблюдателя, и в этом случае он освещён максимально (фаза 1,0). Если фазовый угол ψ = 90°, то для наблюдателя освещена только половина спутника (фаза 0,5). Рис. 4. К определению фазового угла: Н -- наблюдатель, ψ -- фазовый угол. При пролёте ИСЗ по небу наблюдателя, фазовый угол, а с ним и фаза, будут изменяться (см. пример на рис. 5). Как известно, яркость Луны в различных фазах разная -- вычисления [107] показывают, что при фазовом угле ψ = 0° блеск Луны равен -12,3m, при ψ = 90° снизится до -11m, а при ψ = 170° яркость Луны упадёт до -4,1m -- она будет видна в виде тонкого серпика. Фаза тела Ф и фазовый угол ψ связаны простым соотношением: Ф = cos2(ψ/2). Фаза Ф = 1 ("полнолуние") соответствует фазовому углу ψ = 0°, фаза Ф = 0,5 ("первая/третья четверть") соответствует ψ = 90°, а "новолуние" (фаза Ф = 0) -- ψ = 180°. Анимация этого эффекта приведена ниже. Из этого можно заключить, что яркость ИСЗ в течении пролёта будет меняться не только за счёт изменения расстояния "ИСЗ - наблюдатель", но и за счёт изменения фазового угла спутника. Рис. 5. Расчитанное в "Heavensat" изменение фазового угла от времени для ИСЗ "Cosmos-44" (SCN: 876). Время отсчитывается в секундах с момента восхода. [Вверх] Изменение блеска ИСЗ в течении пролёта. Теперь мы вплотную подошли к решению вопроса об вычислении яркости ИСЗ в течении его пролёта по небу наблюдателя. В программе "Heavensat" можно рассчитать эти изменения -- см. рис. 6. Сдвиг графика для "DELTA 1 R/B" обусловлен тем, что в начале траектории он выходил из тени Земли (см. ниже) и блеск его не рассчитывался. Рис. 6. Расчитанное в "Heavensat" изменение блеска от времени для ИСЗ "Cosmos-44" (SCN: 876), "SL-3 R/B" (SCN: 877), "SL-8 R/B" (SCN: 6061) и "DELTA 1 R/B" (SCN: 7735). Время отсчитывается в секундах с момента восхода. Как было сказано выше, яркость спутника будет зависеть от расстояния "r" до наблюдателя и от фазового угла "ψ" ИСЗ. Кроме того, она будет зависеть и от коэффициента отражения поверхности спутника -- его альбедо "A" [108], и от площади "S" отражающей поверхности спутника. 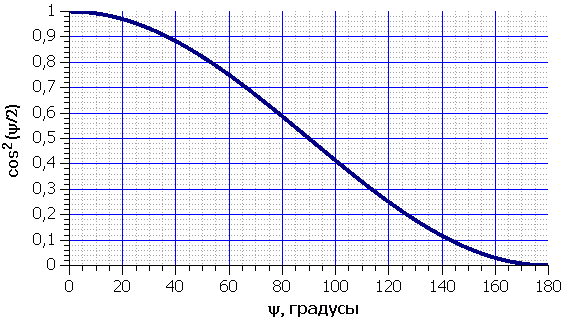Тогда для случая сферического спутника с диффузным отражением (равномерное отражение во все стороны) мы можем записать следующую формулу для освещённости, создаваемой ИСЗ на Земле в точке наблюдения в течении пролёта [101, 104]: ,     (1) где Isun -- освещённость спутника от Солнца вблизи Земли. Более подробно про формулу (1) см. Приложения ("Формулы приведенного блеска для ИСЗ"). На рис. 7 показан график изменения функции cos2(ψ/2). Как и было отмечено выше, из графика видно, что максимальная освещённость создаётся при минимальном фазовом угле ("полнолунии" спутника). [Вверх] Рис. 7. График изменения функции cos2(ψ/2). Из (1), применяя формулу Погсона [109] и значение блеска Солнца (-26,5m) можно выразить зависимость изменения блеска ИСЗ за пролёт: .     (2) Для примера на рис. 8 показано расчитанное по (2) семейство кривых -- яркость ИСЗ "Космос-44" (SCN: 876) при различных значениях альбедо "A", по сравнению с расчётной кривой m(t), выполненной в программе "Heavensat". Как видно, коэффициент отражения поверхности "Космос-44" невелик -- около 10%. Рис. 8. Семейство кривых блеска ИСЗ "Космос-44" (SCN: 876) при разных значениях альбедо. [Вверх] Очень важно отметить, что формула (2) применима только для случая сферического спутника с диффузным отражением. Это всего лишь простейшая модель отражения, и на практике она не реализуется -- очень мало на орбите Земли сферических спутников, без "крыльев" панелей солнечных батарей, антенн и т.д. -- все эти дополнительные элементы вносят изменения в вид т.н. фазовой функции "F(ψ)". В нашем простейшем случае фазовая функция имеет вид F(ψ) = cos2(ψ/2). На практике же для каждого ИСЗ определяется своя фазовая функция -- только тогда наблюдаемое изменение блеска спутника и расчитанное будут близки. Если значение альбедо А заранее не известно, то часто по результатам фотометрии ИСЗ определяют т.н. эффективную площадь, равную произведению альбедо на реальную площадь отражающей поверхности, т.е. 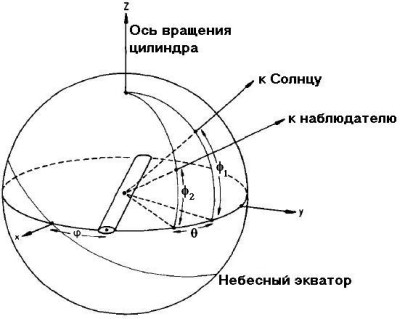A·S В качестве примера других видов фазовых функций рассмотрим цилиндрический спутник (см. рис. 9) [141], как наиболее часто встречающуюся геометрию ИСЗ. Введём понятие спутниковой системы координат -- тройка осей X, Y и Z, в центре пересечения которых находится центр цилиндра. Плоскость XY перпендикулярна оси вращения спутника (т.е. ИСЗ вращается относительно оси Z в плоскости XY), а ось X направлена в восходящий узел линии пересечения плоскости земного экватора и плоскости вращения ИСЗ (плоскость XY). Тогда φ1 -- это "широта" Солнца в спутниковой системе координат, а φ2 -- "широта" наблюдателя на поверхности Земли. Разность этих "широт" обозначим как θ. Рис. 9. Спутниковая система координат [141]. Тогда для полированной сферы, полированного и диффузного цилиндра и пластинки можно ввести фазовые функции F(ψ), показанные в Табл. 1. Таблица 1. Вид фазовых функций для некоторых отражающих поверхностей [142]. [Вверх] В Таблице 1 в примечаниях также указаны минимальные и максимальные значения функции при вспышках. При этом параметр Δ является углом растра конуса отражения, т.е. задаёт угловую ширину "солнечного зайчика", посылаемого спутником на Землю. Минимальное значение Δ≈0.5° определяется угловыми размерами солнечного диска. На рис. 10 показаны теоретические кривые изменения приведенного блеска ИСЗ (см. ниже пункт "Приведенная звёздная величина ИСЗ") в зависимости от фазового угла ψ для разных отражающих поверхностей. Как видно из графиков, зеркальная сфера (кривая 6) будет иметь бОльшую яркость, чем диффузная (кривая 1), только при фазовом угле ψ>≈90°, а при меньших фазовых углах более яркой будет диффузная сфера. Диффузная пластина (кривая 4) даёт самые яркие блики. 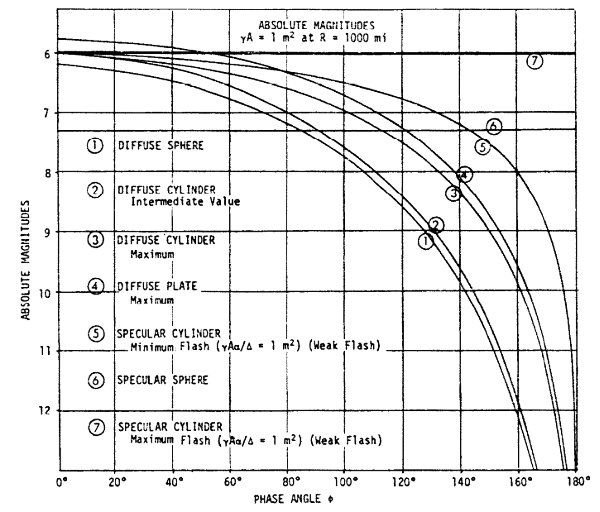Рис. 10. Теоретические кривые зависимости приведенного блеска ИСЗ как функция фазового угла ψ для различных отражающих поверхностей (абсолютный блеск в данном случае определяется для дистанции r = 1000 миль, т.е. 1609 км) эффективной площади A·S = 1 м2 [142]. [Вверх] В заключение пункта отметим ещё один важный момент, влияющий на изменение блеска ИСЗ. Всем известно, что чем ниже находится Солнце у горизонта, тем оно краснее -- достаточно полюбоваться закатом, чтобы в этом ещё раз убедиться. Но любоваться закатом мы можем ещё и потому, что яркость Солнца вблизи горизонта сильно уменьшена по сравнению с полуденной яркостью -- на закате Солнце не слепит нам глаза, хотя днём на него невозможно смотреть, настолько оно яркое. Связано это с тем, что чем ближе Солнце к горизонту, тем через бОльший слой воздуха проходят его лучи. Синие лучи рассеиваются, остаются жёлто-красные, дающие характерный цвет закатного Солнца. Кроме этого, за счёт рассеивания и поглощения солнечных лучей, яркость диска также снижается. Поглощение света в атмосфере характерно для всех космических тел, в том числе и для ИСЗ. Величина поглощения (в звёздных величинах) в зависимости от элевации (угловой высоты) светила над горизонтом показана на рис. 11, построенном на основе данных [105]. График построен относительно поглощения света в зените, которое для области длин волн максимальной чувствительности глаза человека (~550 нм) составляет всего 0,21m [105]. Данные справедливы для высоты 0 м над уровнем моря при давлении 760 мм рт. ст. Рис. 11. Уменьшение яркости светил в зависимости от их элевации. Из графика видно, что при элевации ИСЗ около 10° атмосфера снизит его блеск на 1m, а при элевации 20° атмосфера снизит блеск всего на 0,43m. Отсюда становится понятно, что фотометрические наблюдения ИСЗ нужно выполнять при элевациях не менее 20°-30°. В астрономии точную фотометрию не проводят при высоте светил менее 45°-50°, но для наших любительских приложений можно эту планку немного снизить. На рис. 12 показаны два графика изменения блеска при учёте атмосферного поглощения света и без него (расчёт кривой m(t) выполнен в программе "Heavensat"). Видно, что учёт атмосферного поглощения приводит к "отклеиванию" зависимости m(t), которое особенно велико в области границ ветвей графика -- когда ИСЗ находится вблизи горизонта. И этот случай -- идеализация, т.к. в атмосфере всегда присутствует пыль и мелкие частицы, дымка, котрые могут весьма значительно увеличить поглощение света на пути от спутника к наблюдателю -- опытные наблюдатели на практике убеждаются, что не каждая ясная ночь имеет одинаково "прозрачное" небо, особенно в городах. Всё это, а также засветка неба удалёнными и локальными источниками освешения приводит к тому, что наблюдатель сможет увидеть ИСЗ только начиная с определёной элевации. Рис. 12. Графики изменения блеска в течении пролёта ИСЗ "Космос-44" (SCN: 876) с учётом атмосферного поглощения света и без него. [Вверх] Приведенная звёздная величина ИСЗ. Теперь настало время перейти к вопросу о значении "постоянного" блеска спутника. Что это за величина, если блеск спутника в течении пролёта всё время меняется? Любителям астрономии хорошо известно понятие абсолютной звёздной величины -- блеск звезды, которую "переместили" на расстояние 10 пк от Земли. Если Солнце переместить на такое расстояние, то его блеск снизится с -26,5m до 4,96m [105]. Знание значения абсолютной звёздной величины светил очень важно, т.к. мы точно знаем расстояние, а значит и светимость данной звезды. Подобную концепцию можно применить и для спутников -- каждый спутник можно характеризовать своей приведенной звёздной величиной m0. Смысл слова "приведенная" означает, что яркость ИСЗ приведена к каким-то стандартным условиям -- к стандартному расстоянию и стандартному фазовому углу. Выбор этих стандартных значений -- дело договорённости. Известный наблюдатель спутников Майкл МакКантс (Mike McCants) на основе любительских наблюдений за блеском спутников составил каталог их приведенных яркостей [111]. Расшифровка значений полей в каталоге дана на web-странице [98]. Самое важное, что на основании измерения блеска ИСЗ в течении пролёта (кривая m(t)) можно вычислить m0. На странице [98] МакКантс даёт следующую формулу для вычисления приведенной звёздной величины ИСЗ: ,     (3) где mr -- блеск ИСЗ в любой момент времени "t" пролёта, когда ИСЗ находится на расстоянии "r" от наблюдателя, r -- расстояние "ИСЗ-наблюдатель", ψ -- фазовый угол спутника в момент "t". Определяя значение блеска mr спутника в момент времени "t", и вычисляя расстояние "r" и фазовый угол "ψ" для этого момента времени, мы получаем набор значений приведенного блеска m0. В идеале эти значения должны быть одинаковы (ведь приведенный блеск -- это фиксированная характеристика данного ИСЗ, ни от чего не зависящая!). Но формула (3), как и (2), выведена для случая сферического спутника с диффузным отражением. Кроме того, неточность орбитальных элементов будет приводить к ошибкам в определении расстояния до наблюдателя и текущего значения фазового угла. По этой причине величины m0, вычисленные по данным фотометрии для каждой точки трека ИСЗ, будут отличаться. Выход из положения один -- усреднить значения m0 и полученная усреднённая величина < m0 > и будет приведенным блеском данного ИСЗ. Происхождение формулы (3) можно понять, если использовать формулу (1) и учесть, что приведенное значение m0 МакКантс выводит для расстояния r0 = 1000 км и фазового угла ψ0 = 90°. В итоге можно получить формулу: .     (4) Подробный вывод формулы (4) дан в Приложених ("Формулы приведенного блеска для ИСЗ"). Не смотря на кажущееся отличие (3) от (4), в действительности они полностью идентичны. В заключении пункта приведём следующую иллюстрацию. Пусть мы пронаблюдали пролёт ИСЗ и получили 130 точек фотометрии -- таблицу [mri ; ti], т.е. пары чисел яркости и времени измерения яркости (для этой иллюстрации точки фотометрии расчитывались в программе "Heavensat"). На основе полученной таблицы рассчитываем значение m0 для каждой из 130 точек фотометрии и строим гистограмму (рис. 13). Рис. 13. Гистограмма значений приведённой яркости за пролёт ИСЗ. Для построения подобной гистограммы можно использовать "EXEL", бесплатную "QTiPlot" [97] или другие программы обработки данных. В идеале мы должны были бы получить только одно единственное значение m0. Как видно из гистограммы, значение m0 = 5,0m ± 0,05m. На практике это был бы отличный результат. Кстати говоря, программа "Heavensat" использует для расчёта яркости ИСЗ в течении пролёта каталог МакКантса [111] -- заглянув в директорию ./Data/ в файл "mcnames" (это и есть каталог МакКантса), можно увидеть, что значение приведенного блеска для ИСЗ "Космос-44" (SCN: 876) равно 5m, что мы и получили. При реальных измерениях помимо усреднения значений m0 можно использовать метод наименьших квадратов (МНК) [110]. Для этого формулу (4) можно переписать в виде mr = f(ψ,r) + m0 и методом МНК определить единственный неизвестный параметр m0. [Вверх] Тень Земли. Теперь мы рассмотрим ещё одну особенность наблюдения спутников, с которой приходится сталкиваться на практике. Наша Земля освещается Солнцем, и поэтому она отбрасывает позади себя тень -- область пространства, закрытое от солнечных лучей. Тень окружена полутенью -- областью пространства с частично экранированной засветкой солнечными лучами. Образование тени и полутени показано на рис. 14. Рис. 14. Образование тени и полутени Земли. Масштаб не соблюдён. Тень Земли простирается на значительное расстояние -- периодически случающиеся лунные затмения отлично это доказывают, т.к. Луна обращается вокруг Земли на среднем расстоянии 384400 км, т.е. гораздо дальше даже высокоэлиптичных ИСЗ (см. Главу 2: "Какие орбиты и ИСЗ бывают?"). Относительно простые геометрические расчёты показывают, что тень Земли заканчивается (точка "К" на рис. 12) на расстоянии примерно 1382030 км от центра Земли. Радиус полутени в этой точке (отрезок "КЕ") составляет примерно 11870 км, т.е. в 1,9 раза больше радиуса Земли. Спутники летают вокруг Земли на расстояниях гораздо меньших 1,4 млн км, так что всегда есть вероятность вхождения ИСЗ в тень Земли или выход из неё. Определим географические широты подспутниковых точек (т.е. точек на поверхности Земли, в которые проецируется прямая от центра ИСЗ до центра Земли) при выходе и входе ИСЗ из тени Земли (см. рис. 15). Для простоты будем считать, что спутник движется в день весеннего равноденствия (21 марта, когда склонение Солнца δsun = 0°) по круговой, полярной, низкой орбите на высоте "h" над поверхностью Земли. Землю будем считать сферической, схождением тени Земли для низких спутников также пренебрегаем. Тогда получаем следующее: спутник входит в тень Земли в точке С, при этом он проецируется поверхность Земли в точке В. Широта точки "В" -- это угол MOB = α. Из треугольника CAO находим, что cos(β) = AO/OC = R/(R + h), где R -- радиус Земли, h -- высота ИСЗ над поверхностью Земли. Так как угол MOA -- прямой, то широта α = 90° - β, или окончательно: α = 90° - acrcos(R/(R + h)). Для ИСЗ на круговой орбите с высотой h = 500 км широта α = 68° ю.ш.. Подспутниковая точка выхода из тени будет симметричной -- 68° с.ш.. В день зимнего солнцестояния Солнце смещено к югу на величину своего максимального склонения δsun = -23,5°, и тень Земли подымается на этот же угол δsun вверх. Поэтому для ИСЗ на круговой орбите высотой h = 500 км подспутниковая точка входа в тень Земли будет иметь широту α = 68° - 23,5° = 44,5° ю.ш., а точка выходе сместиться к северному полюсу -- 91,5°, т.е. даже перейдёт северный полюс. В день летнего солнцестояния ситуация изменится на обратную. [Вверх] Рис. 15. К определению подспутниковых точек входа/выхода ИСЗ в тень Земли. Эти простые выкладки показывают, что в зависимости от поры года в течении ночи на небе будут присутствовать сектора, закрытые тенью Земли. Результатом этого будет тот факт, что даже при благоприятных условиях наблюдения ИСЗ часть его траектории будет в тени, и он будет либо резко "выскакивать" из тени либо быстро "пропадать" повреди неба, войдя в тень. Летом в средних широтах северного полушария наступает наиболее благоприятный сезон для наблюдения ИСЗ -- тень Земли не подымается высоко над горизонтом в южной части неба, Солнце не заходит глубоко под горизонт, создавая благоприятные условия для наблюдения ИСЗ (доступны малые фазовые углы, а значит и спутники более яркие). Оборотной стороной медали является тот факт, что из-за низкого положения Солнца под горизонтом ночи с середины мая по середину июля в средних широтах не наступают, тёмное время суток минимально и небо не обладает достаточной тёмностью. На рис. 15 показано положение тени и полутени Земли на небе в местную полночь в день летнего солнцестояния (21 июня) для широты 54° с.ш. -- тень Земли не подымается выше 18° над точкой юга (расчёты выполнены в программе "Heavensat"). Рис. 16. Положение тени и полутени Земли на небе в местную полночь в день летнего солнцестояния (21 июня) для широты 54° с.ш.. Зимой ситуация кардинально меняется -- в период, близкий ко дню летнего солнцестояния в местную полночь в средних широтах северного полушария тень Земли закрывает всё небо, Солнце в течение ночи уходит глубоко под горизонт, так что самое благоприятное время для наблюдения ИСЗ -- это вечер и утро. Весной и осенью ситуация представляет собой нечто среднее между зимой и летом -- тень Земли закрывает большую часть неба в местную полночь, но длительность периода видимости спутников больше, чем зимой. На рис. 17 показано положение тени и полутени Земли на небе в местную полночь в день весеннего равноденствия (21 марта) для широты 54° с.ш. -- тень Земли закрывает почти всё небо с юга, не доходя до точки севера 25°. 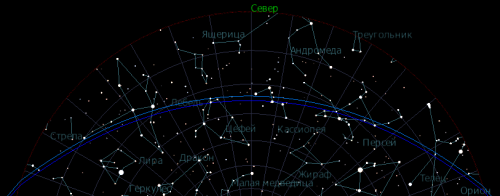Рис. 17. Положение тени и полутени Земли на небе и местную полночь в день весеннего равноденствия (21 марта) для широты 54° с.ш.. Гораздо удобнее смотреть положение тени в программе "Тень & Спутник" [113] -- программа рисует "сетку" спутников на небе и отображает положение тени Земли и фазы спутников (см. рис. 18), а также рассчитывает зенитное расстояние края тени ("Минимальное z" и "Максимальное z" на рисунке) -- см. рис. 15, к примеру, это угол ZFD и ZFC соответственно. 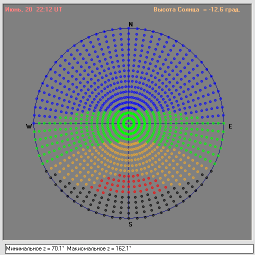Рис. 18. Положение тени и полутени Земли на небе и местную полночь в день летнего солнцестояния (21 июня) для широты 54° с.ш. и долготы 27,5° в.д. по данным программы "Тень & Спутник". [Вверх] Если бы Земля не имела атмосферу, то любой объект в тени Земли был бы абсолютно тёмным (не считая освещённости от звёзд, которая крайне мала). Однако, наличие атмосферной оболочки вокруг Земли приводит к тому, что солнечные лучи преломляются на лимбе Земли и часть солнечных лучай попадает в область тени (см. рис. 19). Угол преломления равен примерно 2° [102]. Любителя астрономии хорошо знают, что даже при полном лунном затмении диск Луны не становится абсолютно чёрным, а имеет тёмно-красный оттенок, наличие которого как раз обусловленно преломлением красных лучеё от Солнца в атмосфере Земли на лимбе. Рис. 19. К определению источника рассеянного света в тени Земли [102]. Малость угла преломления приводит к тому, что конус засветки сходится перед диском Луны. До точки схождения область засветки представляет собой кольцевую зону по краю тени. Получается, что спутник сначала будет входить в полутень Земли, затем в область засветки тени, а только потом в саму тень, где он перестанет отражать свет. Область засветки тени -- очень интересная с точки зрения исследования наличия в атмосфере аэрозолей и прочих примесей, приводящих к дополнительному рассеянию света в атмосфере Земли. На рис. 20 показан график изменения т.н. фактора теневого потемнения (ФТП) [102] -- отношения яркости солнечного диска, частично закрытого диском Земли, к яркости всего солнечного диска. Непрерывная линия -- это расчётная зависимость ФТП от углового расстояния от центра тени Земли (т.н. Гауссова атмосфера), точки -- экспериментальные измерения. Как видно, дополнительные примеся приводят к тому, что поглощение света в центре тени Земли теоретически падает в 100 раз, а на практике -- почти в 1000 раз [106]. 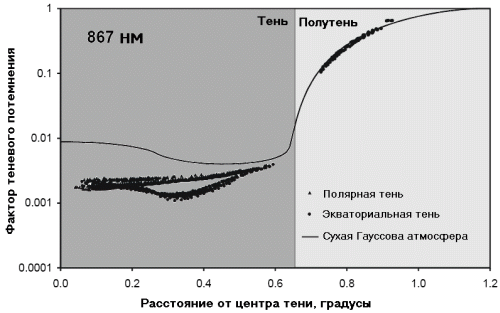Рис. 20. График потемнения Луны в полутени и тени Земли [106]. На рис. 21 приведена составная фотография прохождения Луны через тень Земли при лунном затмении 16-17.08.2008, сделанная любителем астрономии Андреем Олешко (Россия) [103]. На фотографии хорошо видно, что край тени Земли не резкий, а размытый -- это следствие засветки тени при преломлении лучей солнца в атмосфере Земли. Рис. 21. Фотография прохождения Луной тени Земли при лунном затмении 16-17.08.2008 [103]. [Вверх] В случае ИСЗ на высоте 500 км над поверхностью Земли угловое растояние между краем полутени и тени составляет всего 1°-1,5° (см. рис. 17 - 18). Чем ваше орбита спутника, тем больше эта разница -- т.к. конус тени сужается, а конус полутени расширяется с удалением от Земли. И всё же освещённость спутников при вхождении в тень Земли падает довольно быстро практически до нуля даже для самых ярких ИСЗ, таких, как Международная космическая станция (МКС). Пепельный свет Луны, хорошо видимый при малых лунных фазах, в тени Земли отсутствует -- т.к. Солнце находится за земным диском. На рис. 22 представлена фотография входа МКС в тень Земли, снятая Анатолием Григорьевым (г. Яровое, Россия) 14.04.2012 на цифрозеркальный фотоаппарат "Canon EOS 1000D", объектив "Мир-1" 2.8/37, ISO 800, выдержка 32 с. Рис. 22. Вход МКС в тень Земли. Для более подробного рассмотрения трека на рис. 23 показан фотометрический профиль этого трека МКС. Как видно, при входе в тень яркость спутника падает почти линейно на значительном участке трека. 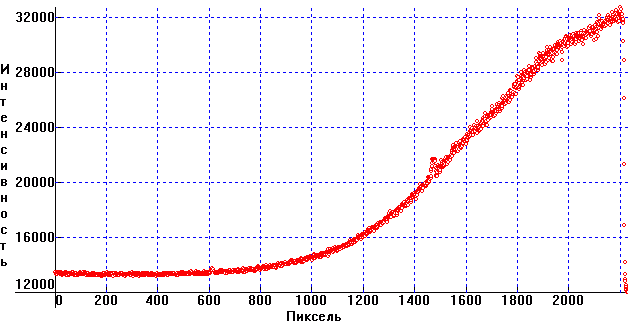Рис. 23. Фотометрическая кривая трека МКС с рис. 22. Ещё одним примером изменения блеска ИСЗ при входе/выходе в тень может служить рис. 24, полученный на основе наблюдений П. Сухова (АО ОНУ, Украина) в Одесской астрономической обсерватории на п.н. Маяки с использованием 50 см телескопа оптической системы Кассегрен, в фокусе которого расположен электрофотометр [100]. ИСЗ "E-Bird"(SCN: 27948), находящийся на геостационарной орбите, в период наблюдений вошёл в тень Земли и почти линейно начал терять свой блеск. Рис. 24. Фрагмент кривой блеска объекта "E-Bird"(SCN: 27948) при входе в тень Земли (в относительных единицах). Интегральный цвет. 05.10.2005, по оси абсцисс отложено всемирное время (UT), по оси ординат -- отсчёты после вычета фона [100]. Выше мы рассмотрели основные особенности движения ИСЗ по небу наблюдателя и изменения блеска спутника, вызванного этими причинами. Теперь можно перейти к рассмотрению отдельных видов фотометрических наблюдений. [Вверх] © BelAstro.Net, Lupus, 15.04.2012